1. Relations
Une relation entre deux ensembles E et F est un sous-ensemble de E × F.
On note : x R y
Propriétés
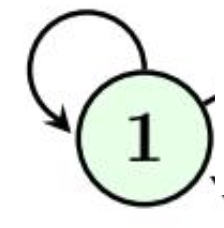
- Réflexive : ∀x ∈ E, xRx
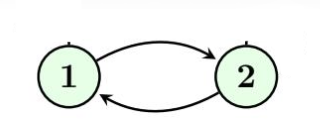
- Symétrique : xRy ⇒ yRx
- Antisymétrique : xRy et yRx ⇒ x = y
- Transitive : xRy et yRz ⇒ xRz
2. Relation d’équivalence
Une relation est une relation d’équivalence si elle est :
- réflexive
- symétrique
- transitive
Classe d’équivalence
La classe d’équivalence de x est :
Cx = { y ∈ E | xRy }
Exemple (modulo n)
x ≡ y (mod n) ⇔ n | (x − y)
3. Relation d’ordre
Une relation est une relation d’ordre si elle est :
- réflexive
- antisymétrique
- transitive
Ordre total et ordre partiel
- Ordre total : tous les éléments sont comparables
- Ordre partiel : certains éléments ne le sont pas
4. Bornes et éléments remarquables
Majorant : ∀x ∈ F, x ≤ M
Minorant : ∀x ∈ F, m ≤ x
Borne supérieure : plus petit des majorants
Borne inférieure : plus grand des minorants
5. Treillis
Un treillis est un ensemble ordonné où tout couple {a,b} admet :
- un supremum a ∨ b
- un infimum a ∧ b
7. Schémas et tableaux (méthodes indispensables)
7.1 Diagramme sagittal
But : représenter une relation entre deux ensembles différents.
Méthode :
- Écrire l’ensemble E à gauche
- Écrire l’ensemble F à droite
- Tracer une flèche x → y si xRy
E F 1 ----> a 2 ----> a 2 ----> b 3
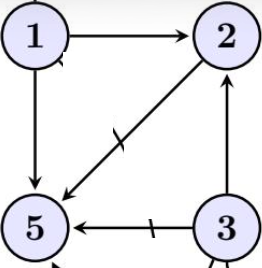
7.2 Graphe orienté
But : relation sur un seul ensemble.
- Chaque élément est un point
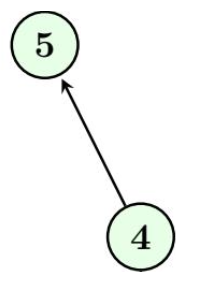
- Flèche de x vers y si xRy
- Boucle si xRx
1 ↺ → 2 → 3
7.3 Diagramme de Hasse (relation d’ordre)
Étapes obligatoires :
- Tracer le graphe orienté
- Supprimer les boucles (réflexivité)
- Supprimer les flèches transitives
- Mettre les plus petits en bas
- Supprimer les flèches (traits simples)
6
/ \
2 3
\ /
1
7.4 Matrice (tableau) de relation
But : représenter une relation sous forme de tableau.
- Éléments en lignes et colonnes
- 1 si xRy, 0 sinon
| R | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 |
Lecture rapide :
- Réflexive : 1 sur la diagonale
- Symétrique : tableau symétrique
- Antisymétrique : pas de 1 symétriques hors diagonale
- Transitive : chemins complétés
7.5 Tableau des classes d’équivalence
- Choisir un élément
- Écrire tous ses équivalents
- Recommencer jusqu’à couvrir E
| Classe | Éléments |
|---|---|
| C₀ | ..., -3, 0, 3, 6, ... |
| C₁ | ..., -2, 1, 4, 7, ... |
| C₂ | ..., -1, 2, 5, 8, ... |